This fixes a typo in the calculation for the Overstraeten/De Man model.
Plus:
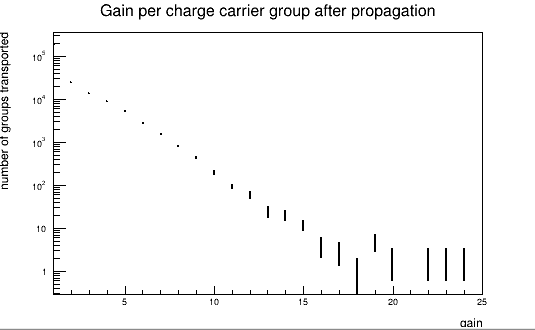
Up to now, in the TransientPropagation new charge carriers were generated when the gain, integrated (gain *= local_gain, actually) for every propagation step, exceeded an integer boundary.
This adds an alternative algorithm, where the probability for impact ionisation is calculated at every step from the local gain only.
By default, the former is used, the latter can be selected via multiplication_probability_based. The additional parameter multiplication_probability_samples (default: 20) allows for dividing the step into substeps, with accordingly reduced generation probability.
This replaces the existing algorithm by a probability based algorithm, where the number of additional charge carriers from impact ionisation is determined at every step from the local gain by drawing a random number from a geometric distribution with x being the local gain.
The approach described in the crossed out text above resulted in dependencies of the gain on the step-size, which is mitigated via the geometric distribution. Dependencies of the gain on the
Examples, 10 events, DepositionGeant4 MIP simulation:
Scenario A: Strikethrough version described above.
Scenario B:
Current master.
Scenario C: This branch.
Results:
Gain distribution, A vs B vs C
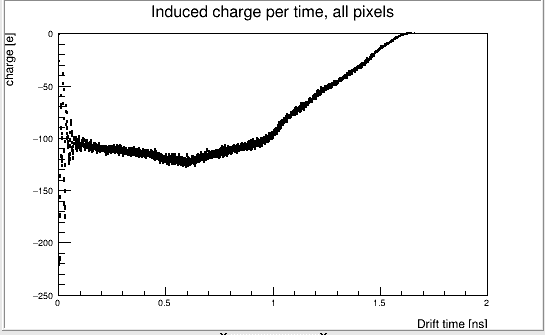
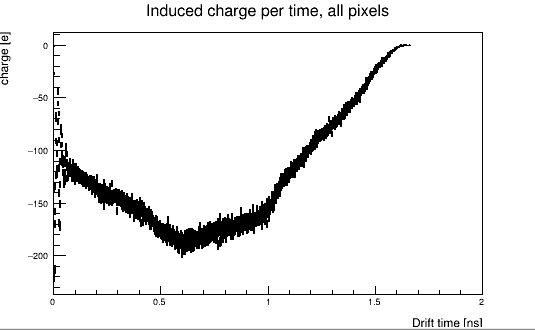
Induced charge, A vs B vs C
