Introduce Possibility for Time-dependent Alignment
A long time ago in a galaxy far, far away...
Sometimes you had this beautiful testbeam campaign where everything is working perfectly and you have day-long runs without any hickup in your DAQ. You do wild parameter scans, remotely performing quasi-online DQM with Corry while sitting on a beach in southern Italy. The full-reco monitoring confirms that your data is nicely correlated and your DUT is fully efficient and hevaing as expected.
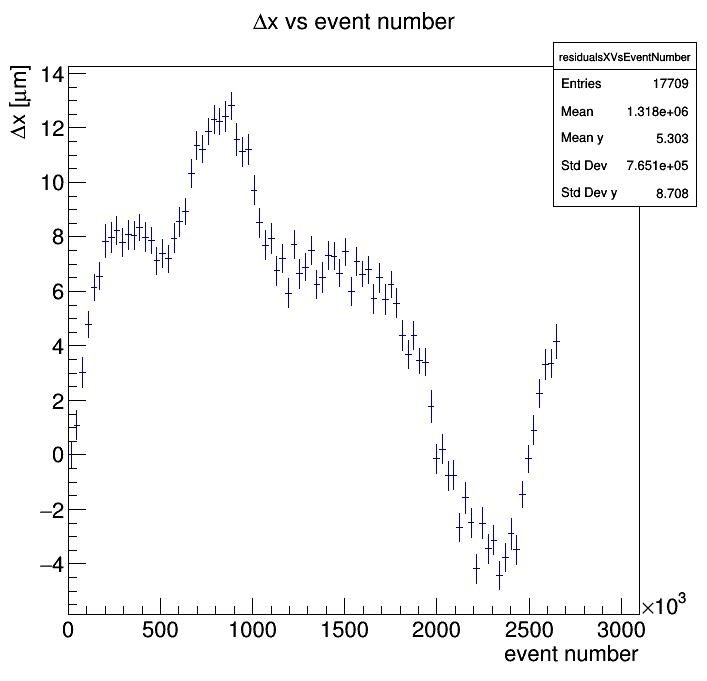
Then testbeam is over and you start looking into more detail into your 12h-long runs...and find some odd effects (as always).
The mean of the residual (i.e. the position fo your detector) changes over time!
(image credit @ffeindt)
Oh dear!
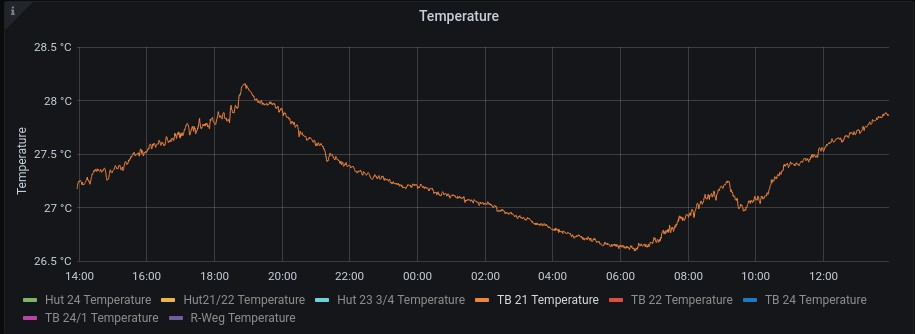
(image credit @pschutze via DESY-II testbeam weather stations)
So far, so good - but how to analyze the data? Chopping them into many small runs seems odd, especially since they will have to be re-aligned individually with relatively low statistics.
Therefore, here the alternative:
Time-Dependent Alignment Constants
With this MR, Corryvreckan gains the possibility of using time-dependent alignment constants. The basic idea of using this feature is the following:
-
Take a run and perform an alignment on it. If this is a dedicated alignment run, perfect. If it is your actual data run, take a small portion of the events at the beginning, with a timescale on which you don't expect any (or only little) drift.
-
Produce a new geometry file with this good alignment constants, and analyze the full run
-
Observe the shift of your residuals in
xandyover the full length of the run -
Perform a fit of some crazy function to it (like, a ninth order polynomial for instance)
-
Go back to your geometry, and instead of (omitting some parameters...)
[MyDUT] orientation = 11.0177deg,186.747deg,-1.07865deg orientation_mode = "xyz" position = -0.251129,0.408979,21.5you now write:
[MyDUT] orientation = 11.0177deg,186.747deg,-1.07865deg orientation_mode = "xyz" position = -0.1*x*x+0.0008*x-sin(0.007*x), 0.408979 + 0.00001*x, 21.5 alignment_update_granularity = 10sinto your geometry file.
How it works
Corryvreckan will take the expression you provide in this case as the x position of your DUT and transform it into a TFormula. From this formula, the alignment constants (positions and resulting transformation matrices) are calculated. The x in the formula represents TIME and is provided in nanoseconds. This means, at the beginning of the run the formulae are evaluated and the initial position is calculated by setting the time to zero, i.e. x = 0.
Each time, the time of your run is incremented, the alignment constants are re-evaluated from these formulae using the current time. In order to not doing this for every single event, the alignment_update_granularity parameter can be used to limit this to e.g. every 10 seconds at most.
All numbers in these formulae have to be provided in framework-internal units, meaning e.g. in mm and ns. Since this is a bit cumbersome in some cases, especially when operating with longer timescales and smaller distances, there is the option of providing parameters separately which can and should use explicit units, e.g. the above example could then become:
position = [0]*x*x+[1]*x-sin([2]*x), [3] + [4]*x, [5]
position_parameters = -100um, 0.8um, 0.007, 408.979um, 0.01um, 21.5mm
alignment_update_granularity = 10sThese arguments are parsed, converted to internal units and placed in the formula in the respective order.
Caveats & Prospects
- This code is still untested on real data, but @asimanca is at it already.
🎉 - If you use time-dependent alignment and then run the alignment procedure on the data, expect funny results.
😄 -
@pschutze was not very happy with the
TFormulaapproach and suggested using a matrix with time ranges and shifts. Also a nice option, I am open to receiving merge requestsⓂ